Pentingnya Memahami Matkul Metode Numerik dalam Pengaplikasian Metode Numerik
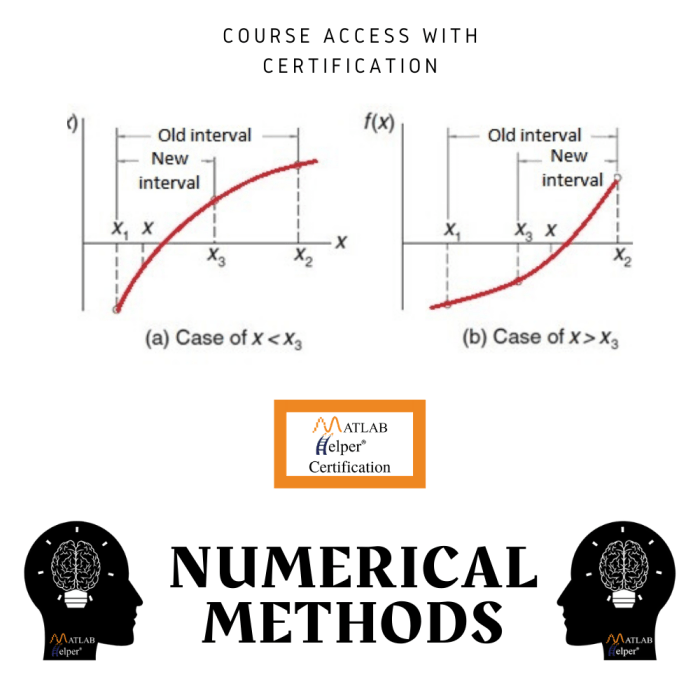
Matkul metode numerik – Matakuliah metode numerik merupakan mata kuliah yang penting dalam dunia akademis, khususnya dalam ilmu komputer dan teknik. Melalui penerapan konsep dasar dan implementasi metode numerik, mahasiswa akan memperoleh pemahaman mendalam tentang cara mencari solusi numerik untuk masalah matematika yang kompleks.
Metode numerik memiliki berbagai jenis, mulai dari konvergensi, analisis kestabilan, hingga error analysis yang menjadi landasan utama dalam menyelesaikan permasalahan numerik. Dengan mengaplikasikan metode numerik dalam bidang teknik dan riset ilmiah, mahasiswa akan dapat memahami urgensi dan kebutuhan akan penguasaan matakuliah ini.
Konsep Dasar Metode Numerik
Metode numerik adalah metode yang digunakan untuk memecahkan masalah matematika dengan pendekatan numerik atau berbasis angka. Prinsip dasar dari metode numerik adalah mengubah persamaan matematika menjadi bentuk yang dapat dipecahkan menggunakan operasi matematika pada angka-angka yang terbatas. Metode numerik sering digunakan dalam berbagai aplikasi, mulai dari komputasi ilmiah, pemodelan matematika, analisis data, hingga pemecahan masalah teknik dan rekayasa.
Jelaskan prinsip dasar metode numerik
Prinsip dasar dari metode numerik adalah menggantikan persamaan matematika yang rumit dengan pendekatan numerik yang lebih sederhana. Dalam metode numerik, masalah matematika dipecahkan dengan menggunakan pendekatan berbasis angka dan algoritma tertentu untuk mendapatkan solusi perkiraan yang cukup akurat.
Identifikasi aplikasi metode numerik dalam pemecahan masalah matematika
- Pemecahan persamaan diferensial
- Interpolasi dan ekstrapolasi data
- Integrasi numerik
- Optimisasi numerik
- Pemodelan matematika
Rangkum pentingnya memahami konsep dasar metode numerik
Memahami konsep dasar metode numerik sangat penting karena dapat membantu dalam pemecahan masalah matematika yang kompleks secara efisien dan akurat. Dengan memahami dasar-dasar metode numerik, seseorang dapat mengembangkan algoritma yang tepat dan efektif untuk menyelesaikan berbagai masalah matematika di berbagai bidang aplikasi.
Implementasi Metode Numerik: Matkul Metode Numerik
Metode numerik adalah teknik matematika yang digunakan untuk menyelesaikan masalah matematika yang sulit atau tidak mungkin diselesaikan secara analitik. Dalam implementasi metode numerik, terdapat langkah-langkah yang harus diikuti untuk menyelesaikan permasalahan nyata.
Jelaskan Langkah-langkah Implementasi Metode Numerik pada Permasalahan Nyata
Implementasi metode numerik pada permasalahan nyata dimulai dengan merumuskan masalah secara matematis, kemudian memilih metode numerik yang sesuai. Selanjutnya, dilakukan iterasi menggunakan algoritma yang telah dirancang hingga diperoleh solusi numerik yang cukup akurat. Terakhir, dilakukan analisis terhadap solusi yang diperoleh untuk memastikan keabsahan hasil.
Rancang Contoh Penerapan Metode Numerik dalam Penyelesaian Persamaan Diferensial
Misalkan terdapat persamaan diferensial yang sulit untuk diselesaikan secara analitik, seperti persamaan diferensial parsial. Dalam hal ini, kita dapat menggunakan metode numerik seperti metode Euler atau metode Runge-Kutta untuk mencari solusi numerik persamaan diferensial tersebut. Dengan membagi domain persamaan menjadi grid dan melakukan iterasi, kita dapat menemukan solusi numerik yang mendekati solusi sebenarnya.
Buat Tabel Perbandingan Hasil antara Metode Numerik yang Berbeda
Untuk membandingkan hasil antara metode numerik yang berbeda, kita dapat membuat tabel yang berisi hasil perhitungan dari masing-masing metode. Tabel tersebut dapat mencakup nilai-nilai numerik, error relatif, serta konvergensi dari setiap metode numerik yang digunakan. Dengan membandingkan tabel tersebut, kita dapat mengevaluasi keakuratan dan keefektifan dari masing-masing metode numerik dalam menyelesaikan permasalahan yang sama.
Jenis-Jenis Metode Numerik
Metode numerik adalah teknik matematika yang digunakan untuk menyelesaikan masalah yang sulit atau tidak dapat diselesaikan dengan cara analitik. Terdapat berbagai jenis metode numerik yang umum digunakan dalam berbagai bidang ilmu, seperti teknik sipil, teknik elektro, dan ilmu komputer.
Metode Numerik Iteratif dan Langsung
Metode numerik dapat dikelompokkan menjadi dua jenis utama, yaitu metode iteratif dan metode langsung. Perbedaan antara keduanya terletak pada cara pendekatan dan penyelesaian masalah yang diberikan.
- Metode Numerik Iteratif: Metode ini melibatkan pendekatan bertahap untuk mendekati solusi yang akurat. Proses iterasi diulang secara berulang hingga solusi konvergen ke nilai yang diinginkan. Metode ini sering digunakan untuk masalah yang kompleks dan memerlukan pendekatan berulang.
- Metode Numerik Langsung: Sebaliknya, metode langsung langsung menghasilkan solusi akhir tanpa memerlukan iterasi berulang. Metode ini cocok untuk masalah yang dapat diselesaikan secara langsung dengan serangkaian operasi matematika yang terdefinisi dengan jelas.
Kelebihan dan Kekurangan Metode Numerik
Berikut adalah beberapa kelebihan dan kekurangan dari masing-masing jenis metode numerik:
| Metode Numerik | Kelebihan | Kekurangan |
|---|---|---|
| Iteratif | Mampu menyelesaikan masalah kompleks yang sulit dilakukan secara analitik. | Membutuhkan waktu komputasi yang lebih lama karena proses iterasi berulang. |
| Langsung | Memberikan solusi akhir secara cepat tanpa memerlukan iterasi berulang. | Tidak dapat digunakan untuk masalah yang kompleks dan memerlukan pendekatan berulang. |
Konvergensi Metode Numerik
Konvergensi dalam konteks metode numerik merupakan konsep penting yang menggambarkan sejauh mana suatu metode numerik mendekati solusi yang akurat seiring dengan peningkatan iterasi. Semakin cepat suatu metode numerik konvergen, semakin efisien waktu dan sumber daya yang digunakan.
Faktor-Faktor yang Mempengaruhi Konvergensi Metode Numerik
Faktor-faktor yang memengaruhi konvergensi metode numerik antara lain adalah:
- Jenis Metode Numerik: Setiap metode numerik memiliki tingkat konvergensi yang berbeda-beda, seperti metode Newton-Raphson yang konvergen secara cepat.
- Initial Guess: Nilai awal yang digunakan dalam iterasi juga mempengaruhi konvergensi. Initial guess yang jauh dari solusi sejati dapat memperlambat konvergensi.
- Linearitas Masalah: Masalah yang lebih linear cenderung memiliki konvergensi yang lebih cepat dibandingkan masalah yang non-linear.
Contoh Perhitungan Konvergensi Metode Numerik dengan Grafik
Sebagai contoh, kita akan membandingkan konvergensi metode iterasi sederhana dengan metode Newton-Raphson. Dengan menggunakan grafik, kita dapat memvisualisasikan perbedaan dalam tingkat konvergensi antara kedua metode tersebut.
Analisis Kestabilan Metode Numerik

Pada dunia komputasi, menganalisis kestabilan metode numerik memiliki peran yang sangat penting. Hal ini bertujuan untuk memastikan bahwa hasil perhitungan yang diperoleh dari metode numerik tidak terpengaruh oleh kesalahan pembulatan, kesalahan pemotongan, atau faktor lain yang dapat mengurangi akurasi dan keandalan hasil.
Jelaskan Pentingnya Menganalisis Kestabilan Metode Numerik
Pentingnya menganalisis kestabilan metode numerik terletak pada kebutuhan untuk memastikan bahwa hasil perhitungan yang diperoleh konsisten dan dapat diandalkan. Dengan menerapkan analisis kestabilan, kita dapat mengidentifikasi potensi kesalahan yang mungkin terjadi selama proses perhitungan dan mengambil langkah-langkah yang diperlukan untuk meminimalkan dampaknya.
Identifikasi Kriteria Kestabilan Metode Numerik
Ada beberapa kriteria yang digunakan untuk menilai kestabilan metode numerik, antara lain:
- Kestabilan Absolut: Metode numerik dikatakan stabil absolut jika kesalahan yang terjadi selama perhitungan tidak berkembang secara eksponensial.
- Kestabilan Relatif: Metode numerik dikatakan stabil relatif jika kesalahan yang terjadi selama perhitungan tetap dalam batas yang dapat diterima.
- Kestabilan Asimtotik: Metode numerik dikatakan stabil asimtotik jika kesalahan yang terjadi cenderung menghilang seiring dengan pertambahan jumlah langkah perhitungan.
Susun Contoh Perhitungan Kestabilan Metode Numerik
Misalkan kita memiliki persamaan diferensial y’ = 2y dengan kondisi awal y(0) = Kita akan menggunakan metode Euler untuk mengevaluasi solusi numeriknya. Dengan langkah iterasi h = 0.1, maka solusi numeriknya adalah:
y(0.1) = y(0) + h
- f(0, 1) = 1 + 0.1
- 2
- 1 = 1.2
y(0.2) = y(0.1) + h
- f(0.1, 1.2) = 1.2 + 0.1
- 2
- 1.2 = 1.44
dan seterusnya…
Error Analysis dalam Metode Numerik
Error merupakan bagian penting dalam metode numerik karena dapat mempengaruhi akurasi perhitungan. Terdapat beberapa jenis error yang perlu diperhatikan dalam metode numerik, serta strategi untuk mengurangi error tersebut.
Jenis-Jenis Error dalam Metode Numerik
- Error Absolut: Selisih antara nilai yang dihitung dengan nilai sebenarnya.
- Error Relatif: Perbandingan error absolut dengan nilai sebenarnya.
- Error Pembulatan: Kesalahan yang muncul akibat pembulatan angka.
- Error Truncation: Kesalahan yang terjadi ketika mengabaikan digit yang tidak relevan dalam perhitungan.
Strategi untuk Mengurangi Error dalam Perhitungan Metode Numerik
- Menggunakan metode iterasi yang lebih presisi.
- Menggunakan representasi floating point yang lebih tepat.
- Mengurangi kesalahan pembulatan dengan teknik pembulatan yang lebih cermat.
- Menggunakan algoritma numerik yang lebih stabil.
Tabel Perbandingan Tingkat Error Antara Metode Numerik yang Berbeda
| Metode Numerik | Tingkat Error |
|---|---|
| Metode Newton-Raphson | Rendah |
| Metode Bagi Dua | Sedang |
| Metode Secant | Tinggi |
Aplikasi Metode Numerik dalam Bidang Teknik

Metode numerik adalah teknik matematika yang digunakan untuk memecahkan masalah dalam bidang teknik dengan pendekatan kuantitatif. Dalam bidang teknik, metode numerik sangat penting untuk melakukan analisis dan perhitungan yang akurat dalam perancangan struktur bangunan dan simulasi proses teknik.
Penerapan Metode Numerik dalam Perancangan Struktur Bangunan
Dalam perancangan struktur bangunan, metode numerik digunakan untuk memprediksi perilaku struktur saat diberikan beban tertentu. Contohnya, dengan menggunakan metode elemen hingga, insinyur sipil dapat mensimulasikan bagaimana suatu struktur bangunan akan merespon terhadap gempa bumi atau angin kencang. Dengan demikian, metode numerik membantu dalam mengoptimalkan desain struktur untuk memastikan keamanan dan keandalan bangunan.
Manfaat Integrasi Metode Numerik dalam Simulasi Proses Teknik, Matkul metode numerik
Integrasi metode numerik dalam simulasi proses teknik memungkinkan insinyur untuk memodelkan fenomena fisik yang kompleks secara akurat. Misalnya, dalam proses pembakaran dalam mesin pembakaran dalam, metode numerik dapat digunakan untuk memprediksi distribusi suhu dan tekanan dalam ruang bakar. Dengan demikian, insinyur dapat melakukan optimasi desain untuk meningkatkan efisiensi dan kinerja sistem secara keseluruhan.
Peran Metode Numerik dalam Riset Ilmiah
Metode numerik memainkan peran krusial dalam pengembangan riset ilmiah modern. Dengan kemampuannya untuk menyederhanakan permasalahan kompleks menjadi bentuk yang dapat dipecahkan secara komputasional, metode numerik membantu para peneliti dalam menganalisis data eksperimen dan mendapatkan pemahaman yang lebih dalam tentang fenomena yang mereka teliti.
Analisis Data Eksperimen
Metode numerik digunakan dalam analisis data eksperimen untuk memodelkan dan memprediksi hasil yang mungkin terjadi berdasarkan data yang diperoleh. Dengan mengimplementasikan algoritma numerik yang tepat, para peneliti dapat mengolah data eksperimen menjadi informasi yang bermanfaat dan dapat dipahami.Contoh penerapan metode numerik dalam penelitian ilmiah dapat dilihat dalam studi tentang dinamika fluida. Dengan memanfaatkan persamaan Navier-Stokes yang rumit, para peneliti menggunakan metode numerik seperti finite element method atau finite difference method untuk mensimulasikan aliran fluida di sekitar benda tertentu.
Hasil simulasi ini kemudian dapat digunakan untuk memprediksi perilaku fluida dalam berbagai kondisi, membantu dalam pengembangan teknologi yang lebih efisien dan ramah lingkungan.Dengan demikian, metode numerik memainkan peran penting dalam memajukan riset ilmiah dengan menyediakan alat yang kuat untuk menganalisis data, memodelkan fenomena kompleks, dan mengambil keputusan yang didasarkan pada bukti-bukti kuantitatif.
Tantangan dan Inovasi dalam Metode Numerik
Metode numerik merupakan pendekatan matematis untuk menyelesaikan masalah matematika yang sulit atau tidak mungkin dipecahkan secara analitis. Namun, pengembangan metode numerik tidaklah tanpa tantangan. Berikut ini akan dibahas mengenai tantangan yang dihadapi dalam pengembangan metode numerik, tren inovasi terkini, serta strategi untuk mengatasi tantangan dan menerapkan inovasi dalam metode numerik.
Tantangan dalam Pengembangan Metode Numerik
- Keterbatasan Presisi: Salah satu tantangan utama dalam pengembangan metode numerik adalah keterbatasan presisi dalam perhitungan. Seiring dengan meningkatnya kompleksitas masalah, diperlukan presisi yang tinggi untuk menghindari kesalahan yang signifikan.
- Konvergensi: Masalah konvergensi seringkali muncul dalam penggunaan metode numerik, di mana iterasi yang dilakukan tidak mencapai solusi yang diinginkan dengan cepat atau bahkan bisa tidak konvergen sama sekali.
- Kestabilan Numerik: Kestabilan numerik menjadi tantangan lain dalam pengembangan metode numerik. Perubahan kecil pada data input dapat menghasilkan perubahan yang signifikan pada output, yang dapat menyebabkan ketidakstabilan dalam solusi.
Inovasi dalam Pengembangan Metode Numerik
- Metode Machine Learning: Penerapan teknik machine learning dalam metode numerik telah menjadi tren inovasi terkini. Machine learning dapat digunakan untuk meningkatkan presisi dan efisiensi dalam perhitungan numerik.
- Komputasi Paralel: Penggunaan komputasi paralel atau distribusi komputasi juga menjadi tren inovasi dalam pengembangan metode numerik. Dengan memanfaatkan sumber daya komputasi secara paralel, proses perhitungan dapat dipercepat secara signifikan.
- Optimisasi Algoritma: Inovasi dalam optimisasi algoritma juga menjadi fokus dalam pengembangan metode numerik. Pengembangan algoritma yang lebih efisien dan cepat menjadi kunci dalam mengatasi tantangan konvergensi dan kestabilan numerik.
Strategi untuk Mengatasi Tantangan dan Menerapkan Inovasi
- Peningkatan Presisi: Menggunakan teknik numerik yang lebih canggih dan presisi yang tinggi, serta melakukan validasi secara berkala untuk memastikan keakuratan hasil perhitungan.
- Optimisasi Konvergensi: Melakukan analisis mendalam terhadap masalah konvergensi, memperbaiki parameter iterasi, dan menerapkan teknik konvergensi yang lebih efisien.
- Implementasi Machine Learning: Mengintegrasikan teknik machine learning dalam metode numerik, seperti penggunaan neural networks atau algoritma machine learning lainnya untuk meningkatkan kinerja perhitungan.
Dengan demikian, pemahaman mendalam tentang metode numerik dapat membawa mahasiswa pada tingkat pemikiran yang lebih analitis dan kritis dalam menyelesaikan permasalahan matematika. Melalui penerapan konsep dan teknik metode numerik, mahasiswa akan siap menghadapi tantangan dan inovasi terkini dalam dunia teknologi dan riset ilmiah.



