Matkul logika matematika merupakan mata kuliah yang mempelajari konsep dasar logika untuk memahami dan menganalisis informasi secara sistematis.
Dengan memahami logika matematika, kita dapat mengenali pola-pola pikir yang terstruktur dan menerapkannya dalam berbagai situasi kehidupan sehari-hari.
Konsep Logika Matematika
Logika matematika adalah cabang logika yang berkaitan dengan penerapan prinsip logika dalam matematika. Logika matematika membahas mengenai penalaran matematis yang tepat dan valid. Dalam logika matematika, digunakan simbol-simbol dan aturan logika untuk membuktikan kebenaran suatu pernyataan matematis.Identifikasi elemen-elemen penting dalam logika matematika:
Pernyataan
Merupakan kalimat atau frasa yang bisa dinyatakan benar atau salah.
Kuantor
Simbol yang digunakan untuk menyatakan jumlah atau kisaran elemen dalam suatu himpunan.
Variabel
Simbol yang digunakan untuk merepresentasikan nilai yang belum diketahui.
Konjungsi, Disjungsi, Implikasi, dan Biconditional
Merupakan operator logika yang digunakan untuk menghubungkan pernyataan.
Perbandingan Logika Klasik dan Logika Matematika Fuzzy
Tabel Perbandingan:
| Logika Klasik | Logika Matematika Fuzzy |
|---|---|
| Menggunakan nilai kebenaran tegas (benar atau salah) | Menggunakan nilai kebenaran yang tidak hanya benar atau salah, tetapi juga nilai di antara keduanya (linguistik) |
| Memiliki batasan yang tegas | Tidak memiliki batasan tegas, lebih fleksibel |
| Menggunakan himpunan yang tegas | Menggunakan himpunan fuzzy yang memungkinkan nilai sebagian |
Contoh penerapan logika matematika dalam kehidupan sehari-hari:Penerapan logika matematika fuzzy dalam sistem kendali pintu otomatis. Dalam sistem ini, terdapat sensor yang dapat mendeteksi berbagai tingkatan cahaya, sehingga pintu dapat membuka atau menutup secara otomatis tergantung pada tingkat cahaya yang terdeteksi.
Struktur Kalimat Logika Matematika
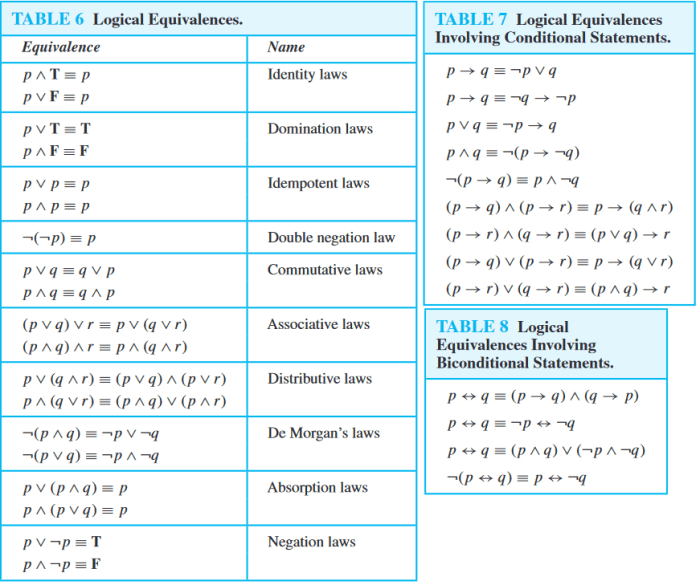
Logika matematika adalah cabang matematika yang mempelajari struktur, prinsip, dan aturan berpikir yang valid. Dalam logika matematika, terdapat struktur kalimat khusus yang digunakan untuk menyatakan pernyataan logis.
Rinci Struktur Kalimat Logika Matematika
Struktur kalimat logika matematika terdiri dari subjek, predikat, dan kuantor. Subjek adalah objek yang diperbincangkan, predikat adalah sifat atau hubungan yang diberikan pada subjek, sedangkan kuantor adalah kata yang menentukan jumlah subjek yang dimaksud.
Jenis-Jenis Operasi Logika
Operasi logika yang umum digunakan meliputi:
- Konjungsi (AND): Menyatakan bahwa kedua pernyataan adalah benar.
- Disjungsi (OR): Menyatakan bahwa salah satu dari dua pernyataan adalah benar.
- Negasi (NOT): Membantah suatu pernyataan.
Contoh Kalimat Logika Matematika
“Jika A adalah bilangan ganjil, maka A + 2 adalah bilangan genap.”
“Semua manusia adalah makhluk hidup.”
Pentingnya struktur kalimat logika matematika adalah untuk memastikan penalaran yang valid dan benar. Dengan struktur yang jelas, setiap pernyataan dapat dianalisis secara logis dan konsisten.
Penerapan Logika Matematika dalam Matkul Terkait
Logika matematika memiliki peran penting dalam berbagai mata kuliah terkait. Hal ini dapat dilihat dalam matematika diskrit, pemrograman komputer, perbandingan dengan logika proposisional, dan pembuktian teorema.
Penerapan Logika Matematika dalam Matematika Diskrit
Logika matematika digunakan secara luas dalam matematika diskrit untuk membantu dalam pemecahan masalah terkait bilangan bulat, himpunan, relasi, dan fungsi. Dengan menggunakan logika matematika, proses pengerjaan soal matematika diskrit dapat lebih terstruktur dan logis.
Relevansi Logika Matematika dalam Pemrograman Komputer, Matkul logika matematika
Logika matematika menjadi dasar dalam pemrograman komputer karena membantu dalam merancang algoritma dan memecahkan masalah secara efisien. Dengan pemahaman logika matematika, seorang programmer dapat menulis kode yang lebih efektif dan efisien.
Perbandingan Logika Matematika dengan Logika Proposisi
| Logika Matematika | Logika Proposisi |
|---|---|
| Mencakup konsep matematika umum | Mencakup pernyataan proposisi |
| Memiliki keterkaitan dengan matematika diskrit | Lebih terfokus pada kebenaran pernyataan |
| Digunakan dalam pemecahan masalah matematika | Terutama digunakan dalam logika formal |
Peran Logika Matematika dalam Pembuktian Teorema
Logika matematika memainkan peran penting dalam pembuktian teorema. Dengan menggunakan aturan logika yang ketat, para matematikawan dapat membuktikan kebenaran dari suatu teorema dan menghasilkan bukti yang kuat dan sahih.
Terakhir: Matkul Logika Matematika
Secara keseluruhan, logika matematika membantu meningkatkan kemampuan berpikir kritis dan analitis, sehingga kita dapat membuat keputusan yang lebih tepat dan efisien.